Угол между диагоналями трапеции равен 60°. Докажите, что сумма длин боковых сторон не меньше, чем длина большего основания.
Решение. Пусть основания трапеции — AD и BC, а диагонали пересекаются в точке O. Рассмотрим сначала более сложный случай, когда 
Лемма. Пусть на стороне произвольного треугольника ABC построен вовне правильный треугольник ABK. Тогда для любой точки P имеет место неравенство 
Доказательство леммы: построим правильный треугольник APM, ориентированный как ABK. Тогда треугольники AKM и ABP равны по двум сторонам и углу, и

Теперь построим параллелограммы BCED и ABDK. Треугольник KDE получается из ABC переносом на вектор  поэтому
поэтому  В силу параллельности
В силу параллельности  и
и 
Имея в виду применить лемму, отложим правильный треугольник CNE вовне CKE. Треугольники KEN и ACE равны по двум сторонам и углу 120° между ними, поэтому  Пользуясь леммой, имеем
Пользуясь леммой, имеем

что и требовалось доказать.
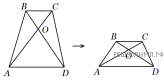
Теперь рассмотрим более простой случай, когда  Приведём этот случай к предыдущему с помощью сжатий. А именно, будем сдвигать BC к AD в направлении, перпендикулярном AD (на рисунке — вниз). При этом углы CAD и CDA уменьшаются, значит,
Приведём этот случай к предыдущему с помощью сжатий. А именно, будем сдвигать BC к AD в направлении, перпендикулярном AD (на рисунке — вниз). При этом углы CAD и CDA уменьшаются, значит,  увеличивается. Можно привести BC в такое положение, что
увеличивается. Можно привести BC в такое положение, что  По уже доказанной части задачи, в этом случае сумма боковых сторон будет не меньше основания. Но боковые стороны в процессе сжатия уменьшились (по теореме Пифагора), а основание не изменилось. Значит, до сжатия это неравенство тем более выполнялось.
По уже доказанной части задачи, в этом случае сумма боковых сторон будет не меньше основания. Но боковые стороны в процессе сжатия уменьшились (по теореме Пифагора), а основание не изменилось. Значит, до сжатия это неравенство тем более выполнялось.
----------
Дублирует задание 1910.