| 1 | 2 | 3 |
| Алюминий | 54% | 7% | 47% |
| Молибден | 8% | 3% | 3% |
| Титан | 36% | 56% | 26% |
На заводе имеются в достаточном количестве три сплава титана, алюминия и молибдена. Все сплавы с примесями. Процентное содержание компонентов в этих сплавах приведено в таблице. Из этих сплавов необходимо приготовить новый сплав, в котором алюминия должно быть не больше 39%, а молибдена — не больше 5%. Какое наибольшее и какое наименьшее содержание титана (в процентах) может быть в этом сплаве?
Решение. Заметим, что как бы ни изготавливали новый сплав, содержание титана в нём будет не больше максимального из содержаний титан а в имеющихся сплавах. Поэтому содержание титан а в любом изготовленном сплаве будет не больше 56%. С другой стороны, сплав 2 подходит под ус ловия на содержание алюминия и молибдена. Значит, наибольшее содержание титана — 56%.
Теперь найдём наименьшее содержание титан а в таком сплаве. Заметим, что если при изготовлении нового сплава мы использовали сплав 1, то можно его заменить на сплав 3: от этого содержание алюминия, молибдена и титана — уменьшится. Поэтому в сплаве с наименьшим содержанием титана не участвует сплав 1.
Сразу отметим, что тогда в таком сплаве будет 3% молибдена, т. е. он подходит под условие на молибден. В сплаве 3 титан а меньше, чем в сплаве 2 , но сплав 3 не подходит под условие н а алюминий . Понятно, что чем меньше мы возьмём сплава 2, тем меньше будет титана в изготовленном сплаве. Возьмём ровно столько, чтобы выполнилось условие на алюминий:  и (x и y — масса сплава 2 и 3 соответственно), откуда
и (x и y — масса сплава 2 и 3 соответственно), откуда  т. е. можно взять 1 часть сплава 2 и 4 части сплава 3. Тогда содержание титана в процентах будет
т. е. можно взять 1 часть сплава 2 и 4 части сплава 3. Тогда содержание титана в процентах будет

Ответ: 32 и 56.
Приведём другое решение.
Пусть взято x и y и  первого, второго и третьего сплава соответственно, приче̄м
первого, второго и третьего сплава соответственно, приче̄м 

 Тогда условия задачи можно записать так:
Тогда условия задачи можно записать так:


Изобразим на координатной плоскости область (см. рис.), удовлетворяющую системе неравенств

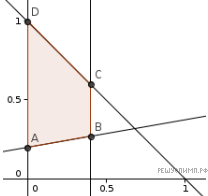
Процентное содержание титана

Легко видеть, что миним ум этого числа достигается в точке A (там наименьший и x, и y ) и равен  Кроме того, при любом фиксированном x мы можем увеличить y до того момента, пока точка не попадёт на от резок CD. На отрезке CD же нас интересует точка с наибольшим y (поскольку содержание титана равно
Кроме того, при любом фиксированном x мы можем увеличить y до того момента, пока точка не попадёт на от резок CD. На отрезке CD же нас интересует точка с наибольшим y (поскольку содержание титана равно  т. е. точка C. В ней содержание титана равно 56 процентов.
т. е. точка C. В ней содержание титана равно 56 процентов.
Комментарий.
При другом выборе переменных (например, x первого сплава,  второго и y третьего) будут получаться другие функции и другие области. При этом решение может стать как чу ть проще, так и немного сложнее. В решении выше специально выбран наиболее «бездумный» путь.
второго и y третьего) будут получаться другие функции и другие области. При этом решение может стать как чу ть проще, так и немного сложнее. В решении выше специально выбран наиболее «бездумный» путь.
Комментарий.
Задача имеет отношение к теме «линейное программирования»: нахождение экстремумов на множествах, задаваемы  системами линейных у равнений и неравенств. Несложно показать, что для линейной функции максиму минимум достигаются в одной из вершин многоугольника множества всех точек, для которых выполняются условия. Тогда задача решается чисто алгоритмически: достаточно пост роить многоугольник, найти все его вершины и в каж дой посчитать значение требуемой функции (так устроено второе решение вы ше).
системами линейных у равнений и неравенств. Несложно показать, что для линейной функции максиму минимум достигаются в одной из вершин многоугольника множества всех точек, для которых выполняются условия. Тогда задача решается чисто алгоритмически: достаточно пост роить многоугольник, найти все его вершины и в каж дой посчитать значение требуемой функции (так устроено второе решение вы ше).
Для произвольных констант такая задача нагружена технически и для олимпиады скорее неудачна. В предложенных вариантах числа подобраны так, чтобы экстремум можно было найти несложными рассуж дениями (так устроение первое решение выше), а не просто технически.
Критерии проверки:| Критерии оценивания | Балл |
|---|
| Верное решение без существенных недочетов | + |
| В целом задача решена, хотя и с недочетами | + − |
| Задача не решена, но есть заметное продвижение | − + |
| Задача не решена, заметных продвижений нет | − |
| Задача не решалась | 0 |
Ответ: 32 и 56.



