
а) Решите уравнение 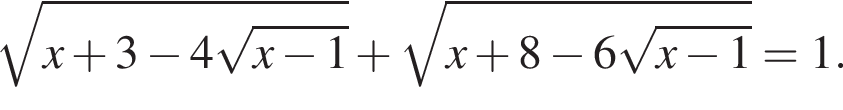
б) Числа  выбираются случайным образом. Найдите вероятность того, что многочлен
выбираются случайным образом. Найдите вероятность того, что многочлен 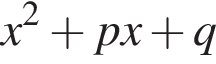 имеет действительные корни.
имеет действительные корни.
в) Докажите, что если не существует треугольника с длинами сторон a, b, c, то нет и треугольника со сторонами
г) Докажите, что треугольник ABC является прямоугольным тогда и только тогда, когда 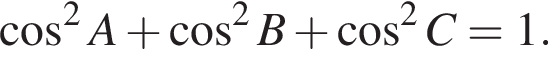
Решение. а) Положим  Относительно новой переменной имеем уравнение
Относительно новой переменной имеем уравнение 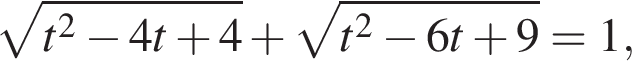
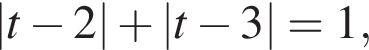
![]() и только они,
и только они, 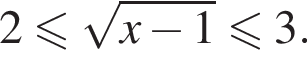
Ответ: 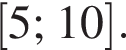
б) Данное уравнение имеет корни тогда и только тогда, когда 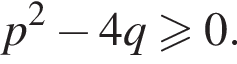 По определению геометрической вероятности, искомая вероятность равна отношению площади множества точек единичного квадрата, координаты которых удовлетворяют неравенству, т. е. площади подграфика функции
По определению геометрической вероятности, искомая вероятность равна отношению площади множества точек единичного квадрата, координаты которых удовлетворяют неравенству, т. е. площади подграфика функции 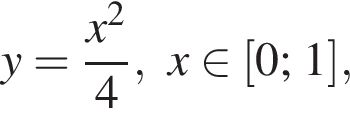 к площади самого этого квадрата. Таким образом, эта вероятность равна интегралу
к площади самого этого квадрата. Таким образом, эта вероятность равна интегралу 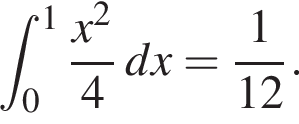
в) Если треугольник с длинами сторон a, b, c не существует, то одно из этих чисел не меньше суммы двух других. Пусть 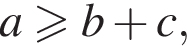 тогда
тогда

г) Прежде всего запишем данное условие в виде
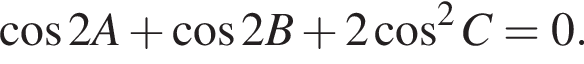
Преобразуем далее:
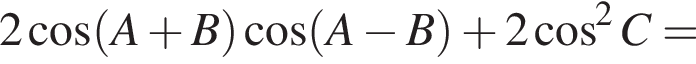
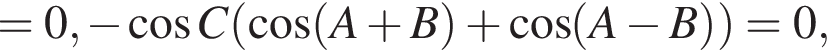
 откуда и следует, что один из углов треугольника — прямой.
откуда и следует, что один из углов треугольника — прямой.| За каждый из четырех пунктов сюжета выставляется одна из следующих оценок: + (3 балла), ± (2 балла), ∓ (1 балл), − (0 баллов) Максимум за сюжет 12 баллов. При этом необходимо руководствоваться следующим. | |
| Критерии оценивания выполнения заданий | Баллы |
|---|---|
| Верное и полное выполнение задания | 3 |
| Ход решения верный, решение доведено до ответа, но допущен один недочет | 2 |
| Ход решения верный, решение доведено до ответа, но допущено два недочета или одна грубая ошибка | 1 |
| Остальные случаи | 0 |
| К недочетам относятся, например: описки, неточности в использовании математической символики; погрешности на рисунках, недостаточно полные обоснования; неточности в логике рассуждений при сравнении чисел, доказательстве тождеств или неравенств; вычислительные ошибки, не повлиявшие принципиально на ход решения и не упростившие задачу, если задача не являлась вычислительной; замена строго знака неравенства нестрогим или наоборот; неверное присоединение либо исключение граничной точки из промежутка монотонности и аналогичные. Грубыми ошибками являются, например: потеря или приобретение постороннего корня; неверный отбор решения на промежутке при правильном решении в общем виде; вычислительная ошибка в задаче на вычисление; неверное изменение знака неравенства при умножении на отрицательное число, логарифмировании или потенцировании и т. п. | |
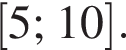
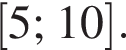
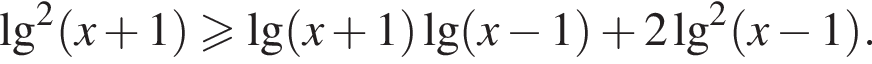
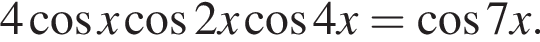
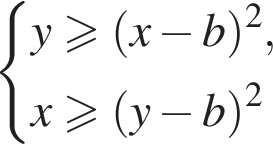
 Поскольку
Поскольку 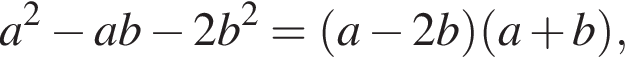 то
то 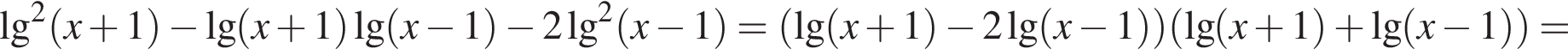
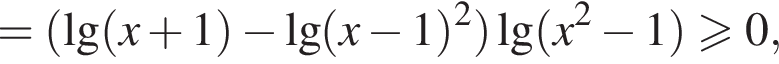
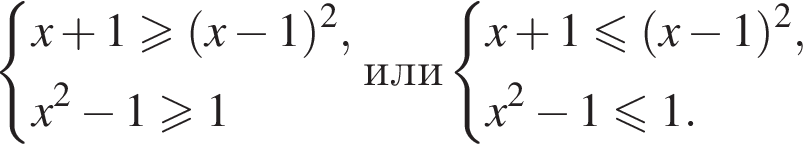
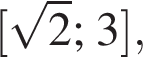 решение второй — отрезок
решение второй — отрезок 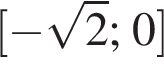 — не лежит в области определения исходного неравенства.
— не лежит в области определения исходного неравенства. 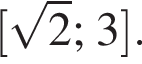
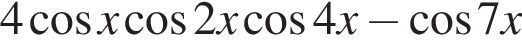 при помощи преобразования произведения косинусов в сумму и наоборот может быть приведено к виду
при помощи преобразования произведения косинусов в сумму и наоборот может быть приведено к виду  откуда
откуда 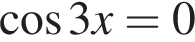 или
или 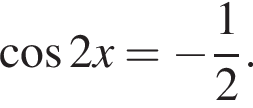
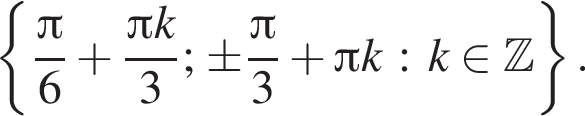
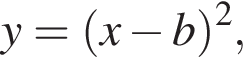 второе — множество точек, лежащих, не левее симметричной ей относительно прямой
второе — множество точек, лежащих, не левее симметричной ей относительно прямой 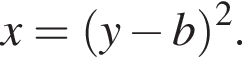 Ясно, что эти множества имеют единственную общую точку тогда и только тогда, когда первая парабола касается прямой
Ясно, что эти множества имеют единственную общую точку тогда и только тогда, когда первая парабола касается прямой 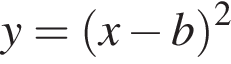 касается прямой
касается прямой 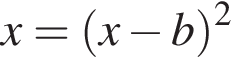 имеет единственное решение. Приравняв нулю дискриминант этого уравнения, получим ответ.
имеет единственное решение. Приравняв нулю дискриминант этого уравнения, получим ответ.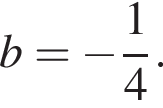
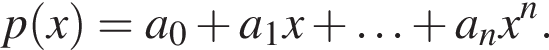
 при всех
при всех 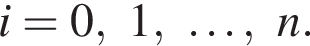
 при всех
при всех 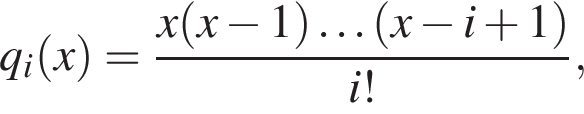
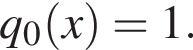 Докажите, что если
Докажите, что если 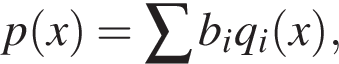 где
где 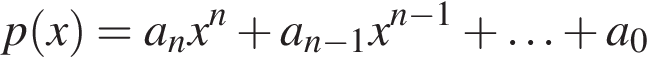 в виде
в виде 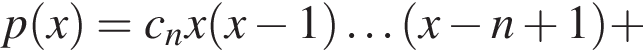
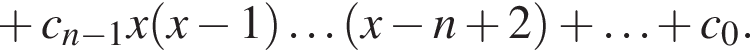
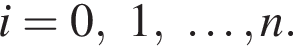 Подставляя в выписанное разложение последовательно числа
Подставляя в выписанное разложение последовательно числа 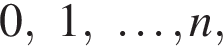 получим систему равенств
получим систему равенств 
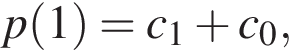
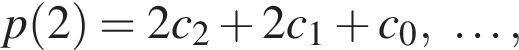
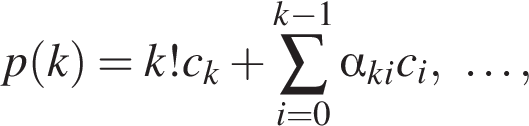
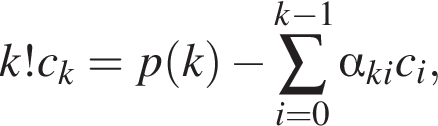
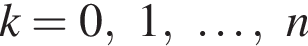 следует рациональность коэффициентов ck (ср. далее с решением пункта в)).
следует рациональность коэффициентов ck (ср. далее с решением пункта в)). 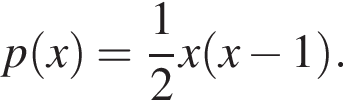
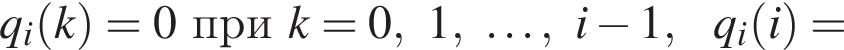
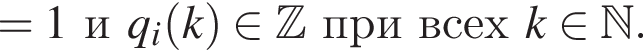
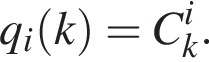
 что
что 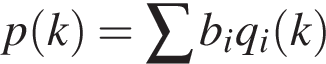 при
при 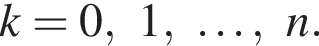
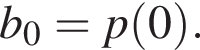 Предположим, что числа
Предположим, что числа 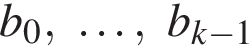 являются целыми. Подставив
являются целыми. Подставив 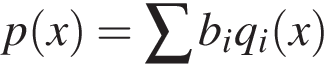 и воспользовавшись отмеченными свойствами многочленов
и воспользовавшись отмеченными свойствами многочленов 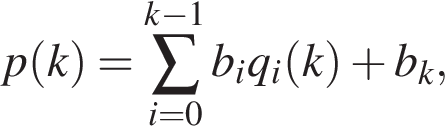
 поэтому второе число больше.
поэтому второе число больше. 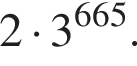 Идея рассуждения: если
Идея рассуждения: если 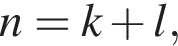 где
где 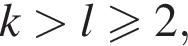 то
то 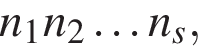 в котором хотя бы одно из чисел ni больше четырех, не может быть наибольшим. Так как
в котором хотя бы одно из чисел ni больше четырех, не может быть наибольшим. Так как  то четверки можно из рассмотрения исключить. Таким образом, наибольшее произведение натуральных чисел с заданной суммой следует искать среди произведений двоек и троек. Осталось заметить, что в силу утверждения предыдущего пункта двоек должно быть как можно меньше.
то четверки можно из рассмотрения исключить. Таким образом, наибольшее произведение натуральных чисел с заданной суммой следует искать среди произведений двоек и троек. Осталось заметить, что в силу утверждения предыдущего пункта двоек должно быть как можно меньше. 
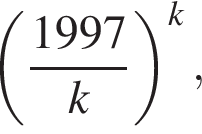 которое, в свою очередь, не превосходит наибольшего значения функции
которое, в свою очередь, не превосходит наибольшего значения функции 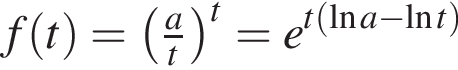 (при
(при 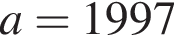 ). Дифференцируя, получаем
). Дифференцируя, получаем 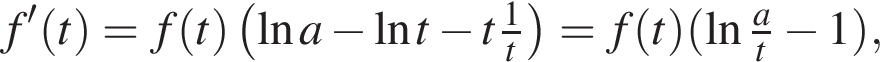
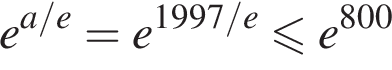 (здесь мы воспользовались тем, что
(здесь мы воспользовались тем, что 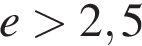 ).
).