Сфера с центром O вписана в трёхгранный угол с вершиной S и касается его граней в точках K, L, M (все плоские углы трёхгранного угла различны). Найдите угол KSO и площадь сечения данного трёхгранного угла плоскостью KLM, если известно, что площади сечений трёхгранного угла плоскостями, касающимися сферы и перпендикулярными прямой SO, равны 4 и 9.
Решение. Обозначим точки пересечения прямой SO со сферой через P и Q (точка P лежит на отрезке SO, а Q — вне него). Пусть радиус сферы равен r. Треугольники OKS, OLS и OMS прямоугольные (углы при вершинах K, L, M прямые, так как касательные перпендикулярны радиусам, проведённым в точку касания). Эти треугольники равны по катету и гипотенузе  SO — общая), следовательно,
SO — общая), следовательно,

(пусть 
 Высоты, опущенные из точек K, L, M на гипотенузу SO, равны, а их основания — одна и та же точка H, лежащая в плоскости KLM (назовём эту плоскость τ). Пусть β и
Высоты, опущенные из точек K, L, M на гипотенузу SO, равны, а их основания — одна и та же точка H, лежащая в плоскости KLM (назовём эту плоскость τ). Пусть β и  касательные плоскости к сфере, проходящие через точки P и Q, а E и F — точки пересечения этих плоскостей с прямой SK. По условию площади сечений трёхгранного угла этими плоскостями равны соответственно
касательные плоскости к сфере, проходящие через точки P и Q, а E и F — точки пересечения этих плоскостей с прямой SK. По условию площади сечений трёхгранного угла этими плоскостями равны соответственно  и
и  Рассмотрим сечение трехгранного угла и сферы плоскостью
Рассмотрим сечение трехгранного угла и сферы плоскостью  (см. рис. и обозначения на нем). Так как SH перпендикулярна HK и SH перпендикулярна HL, то τ и SH — перпендикулярны. Тогда сечения трёхгранного угла плоскостями
(см. рис. и обозначения на нем). Так как SH перпендикулярна HK и SH перпендикулярна HL, то τ и SH — перпендикулярны. Тогда сечения трёхгранного угла плоскостями 
 и
и  — подобные треугольники, плоскости которых параллельны (все они перпендикулярны SO).
— подобные треугольники, плоскости которых параллельны (все они перпендикулярны SO).
Если  — площадь треугольника, получающегося в сечении трёхгранного угла плоскостью KLM, то из подобия
— площадь треугольника, получающегося в сечении трёхгранного угла плоскостью KLM, то из подобия
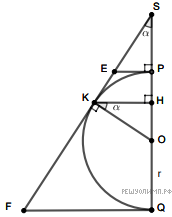

Следовательно,

Тогда

откуда
 и
и 
Отсюда 
Далее,
Значит,






откуда 
Ответ: 

Критерии проверки:Доказано, что плоскость KLM параллельна касательной плоскости — 1 балл.
Найден угол KSO — 2 балла.
Найдена площадь — 2 балла.
Ответ: 

Аналоги к заданию № 826: 833 Все



