CAKD — квадрат со стороной 6. На стороне CD выбирается точка B (BD = 2), а на прямой AD — такая точка E, что периметр треугольника BEC — наименьший из возможных. Затем, на прямой DС отмечается такая точка F, что периметр треугольника FEA — наименьший из возможных. Найти EF.
Решение. Построение и доказательство: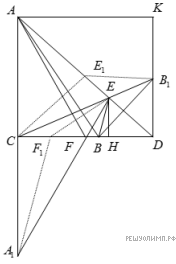
Отметим точку B1 на стороне DK, так
Проведем прямую B1C, которая пересечет AD в точке Е. Периметр треугольника CBE — наименьший, так как из всех возможных точек E1 на прямой AD — сумма длин отрезков 
наименьшая (неравенство треугольника —
и 
Аналогично, отметим точку A1 на стороне AC 
Проведем прямую A1E, которая пересечет CD в точке F.
Периметр треугольника AFE — наименьший, так как из всех возможных точек F1 на прямой AD — сумма длин отрезков 
наименьшая, (неравенство треугольника —
и 
Решение:
Найдем BD и B1D:
Так как треугольники ACE и B1ED подобные 
вертикальные и 
то
Пусть прямая EH перпендикулярна DC, следовательно, прямоугольные треугольники ACD и EHD подобны 
— общий), тогда
Прямоугольные треугольники FHE и FСА1 подобны 
вертикальные), тогда
Ответ: 
Критерии проверки:| Баллы | |
|---|
| 20 | Обоснованное и грамотно выполненное решение задачи. |
| 16 | При верном и обоснованном ходе решения имеется арифметическая ошибка или решение недостаточно обосновано. |
| 12 | При верном ответе нет доказательства минимальности периметра. |
| 4 | Верно начато решение задачи, получены некоторые промежуточные результаты, дальнейшее решение неверно или отсутствует. |
| 0 | Решение не соответствует вышеперечисленным требованиям. |
Ответ: 
