Даны две правильные четырехугольные пирамиды с плоским углом при вершине  Они имеют общую боковую грань и не имеют других общих точек. В пирамиды вписаны шары радиуса r. Третий шар радиуса R касается внешним образом обеих пирамид и вписанных в них шаров. Найдите отношение R к r.
Они имеют общую боковую грань и не имеют других общих точек. В пирамиды вписаны шары радиуса r. Третий шар радиуса R касается внешним образом обеих пирамид и вписанных в них шаров. Найдите отношение R к r.
Решение. 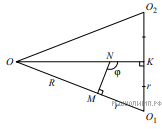 Пусть SABC — первая пирамида, BSC — ее общая боковая грань со второй, O1 и O2 — центры шаров, вписанных в пирамиды, O — центр внешнего шара. Ввиду равенства пирамид вписанные в них шары касаются грани BSC в одной точке K. Так как отрезок O1K перпендикулярен плоскости BSC и отрезок O2K перпендикулярен плоскости BSC, точка K лежит на отрезке O1O2, причем
Пусть SABC — первая пирамида, BSC — ее общая боковая грань со второй, O1 и O2 — центры шаров, вписанных в пирамиды, O — центр внешнего шара. Ввиду равенства пирамид вписанные в них шары касаются грани BSC в одной точке K. Так как отрезок O1K перпендикулярен плоскости BSC и отрезок O2K перпендикулярен плоскости BSC, точка K лежит на отрезке O1O2, причем  Пусть M — точка касания с гранью ASB шара, вписанного в первую пирамиду. В этой же точке касается ASB и внешний шар. Поэтому точка M лежит на отрезке OO1, причем
Пусть M — точка касания с гранью ASB шара, вписанного в первую пирамиду. В этой же точке касается ASB и внешний шар. Поэтому точка M лежит на отрезке OO1, причем  Аналогично получается, что
Аналогично получается, что  Выберем точку N на отрезке OK так, что NM перпендикулярна OO1, и положим
Выберем точку N на отрезке OK так, что NM перпендикулярна OO1, и положим  (см. верхний рисунок). Тогда
(см. верхний рисунок). Тогда



Покажем, что  — угол между гранями ASB и BSC. Действительно, O1K и O1M — paдиусы шара, вписанного в первую пирамиду, откуда отрезок O1M перпендикулярен плоскости ASB и отрезок O1K перпендикулярен плоскости BSC. Значит, отрезок BS и плоскость MNK перпендикулярные. Кроме того, прямая MN лежит в плоскости ASB, а KN — в плоскости BSC.
— угол между гранями ASB и BSC. Действительно, O1K и O1M — paдиусы шара, вписанного в первую пирамиду, откуда отрезок O1M перпендикулярен плоскости ASB и отрезок O1K перпендикулярен плоскости BSC. Значит, отрезок BS и плоскость MNK перпендикулярные. Кроме того, прямая MN лежит в плоскости ASB, а KN — в плоскости BSC.
Пусть  и
и  Опустим из точек A и C перпендикуляры на ребро BS. Они придут в одну точку L, так как треугольники ASB и BSC равны. По доказанному
Опустим из точек A и C перпендикуляры на ребро BS. Они придут в одну точку L, так как треугольники ASB и BSC равны. По доказанному  Заметим, что
Заметим, что 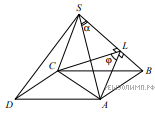



По теореме косинусов для треугольника ALC:

Поэтому

Ответ: 
Ответ: 
Они имеют общую боковую грань и не имеют других общих точек. В пирамиды вписаны шары радиуса r. Третий шар радиуса R касается внешним образом обеих пирамид и вписанных в них шаров. Найдите отношение R к r.



