Решение. Процедура построения сечения десятигранника плоскостью ASU состоит из двух шагов:
1) Отмечаем точку K пересечения прямых SU и QR, точку $L$ пересечения прямых SU и WV и точку M пересечения прямых SU и PW;
2) Проводим прямую AM, точку ее пересечения с ребром DW обозначим G, проводим прямую GL; точку ее пересечения с ребром DV обозначим F, проводим прямую AK, точку ее пересечения с ребром BR обозначим E.
Шестиугольник AESUFG и будет сечением.
Поскольку, по условию, ABCD — квадрат, а DAPW, ABRQ, BCTS и CDVU прямоугольники, то

Кроме того, величины всех углов восьмиугольника PQRSTUVW равны между собой, поэтому, по теореме о сумме величин углов многоугольника, они равны  Из этого вытекает, что прямые ST и WP параллельны, прямые QR и UV параллельны, прямые QR и ST перпендикулярны.
Из этого вытекает, что прямые ST и WP параллельны, прямые QR и UV параллельны, прямые QR и ST перпендикулярны.
Это означает, что четырехугольник IJXY, образованный прямыми QR, ST, UV и WP — прямоугольник. Ясно, что треугольники PIQ, RJS, TXU и WYP прямоугольные и равнобедренные. Обозначив 


 и учитывая, что
и учитывая, что  и
и  имеем
имеем

откуда находим

то есть IJXY квадрат. Далее, рассмотрим точки A1, B1, C1 и D1, являющиеся ортогональными проекциями точек A, B, C и D на плоскость PQRSTUVW соответственно. По теореме о трех перпендикулярах, 






Поскольку A1B1C1D1 тоже квадрат, то точки Q, A1, D1, V лежат на одной прямой, из чего следует  Итак,
Итак,  то есть
то есть

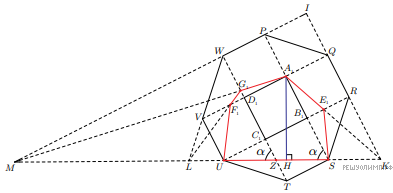
Обозначив ортогональные проекции точек E, F и G на плоскость PQRSTUVW буквами E1, F1 и G1 соответственно, получаем чертеж.
Мы знаем, что

Из вышеприведенных рассуждений следует, что длины всех отрезков A1P, A1Q, B1R, B1S, C1T, C1U, D1V и D1W тоже равны 1.
Из подобия треугольников UB1S и URK имеем

откуда  Затем, из подобия треугольников RKE и B1A1E находим
Затем, из подобия треугольников RKE и B1A1E находим

Пусть  Из треугольника UB1S получаем
Из треугольника UB1S получаем

и из треугольника MPS имеем  Далее, из подобия треугольников MPA1 и MWG1 вытекает
Далее, из подобия треугольников MPA1 и MWG1 вытекает

Из треугольника MWZ находим  после чего, из подобия треугольников LWZ и LVU получаем
после чего, из подобия треугольников LWZ и LVU получаем

Наконец, записывая теорему Менелая для треугольника WD1V и секущей G1F1, имеем



Теперь можно вычислить площадь S* ортогональной проекции A1E1SUF1G1 построенного сечения на плоскость PQRSTUVW:



Опустим на прямую SU перпендикуляр A1H. Его длина равна  а угол A1HA (так как
а угол A1HA (так как  будет углом β между плоскостью сечения и плоскостью основания PQRSTUVW. Тогда, если обозначить искомое расстояние (длину отрезка AA1) за h, то, с одной стороны,
будет углом β между плоскостью сечения и плоскостью основания PQRSTUVW. Тогда, если обозначить искомое расстояние (длину отрезка AA1) за h, то, с одной стороны,

и, с другой стороны,

Решая уравнение  находим
находим 
Ответ: 
Найдите расстояние между его основаниями.
Найдите угол между ребром TC плоскостью ABC.



