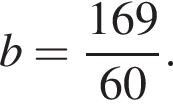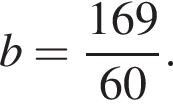Окружность, центр которой лежит на прямой y = b, пересекает параболу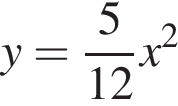 
хотя бы в трёх точках; одна из этих точек – начало координат, а две из оставшихся лежат на прямой 
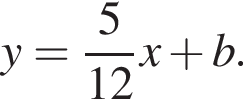Найдите все значения b, при которых описанная конфигурация возможна.
Решение. Рассмотрим сначала 
Обозначим начало координат через 
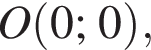центр окружности через 
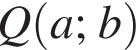(так как он лежит на прямой 
его ордината равна b); точки пересечения прямой с параболой через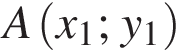 
и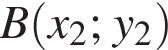 
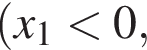
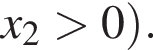Пусть также 
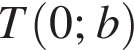— точка пересечения данной прямой с осью ординат, C — точка пересечения окружности с осью ординат,
Треугольник QOC равнобедренный 
как радиусы), QT — его высота, следовательно, QT также и медиана, 
поэтому точка C имеет координаты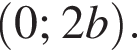 
Опустим из точки A перпендикуляр 
на ось ординат. Тогда 
есть угол наклона прямой, его тангенс равен 
Отсюда 
и
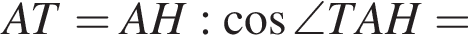
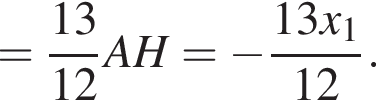
Аналогично находим, что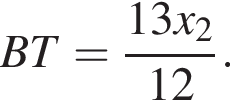 
Прямые AB и OC — две хорды данной окружности. По теореме о пересекающихся хордах*
то есть
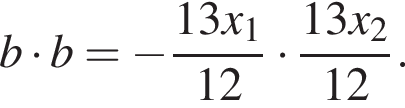
Абсциссы 
и 
точек пересечения прямой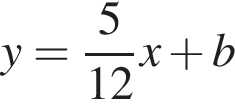 
и параболы 
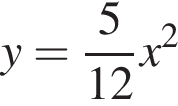определяются уравнением
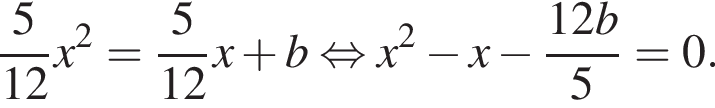
По теореме параболы 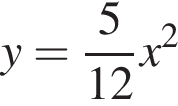определяются уравнением
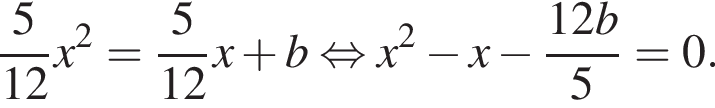
По теореме Виета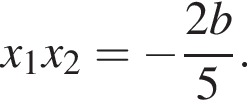 
Значит,
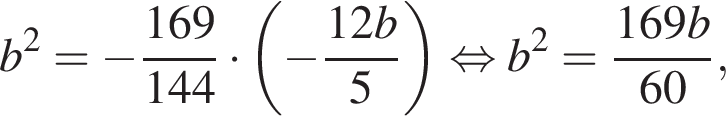
откуда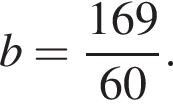 
Значение 
не подходит, так как при этом заданная прямая принимает вид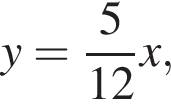 
то есть проходит через начало координат.
При 
(естественно, мы рассматриваем только те b, при которых прямая и парабола имеют две точки пересечения) оба числа и положительны. Точка T является серединой отрезка 
(сохраняем все обозначения первого случая). Тогда с одной стороны выходит, что точка T — середина хорды OC, т. е. лежит внутри окружности. С другой стороны, точки A и B лежат на окружности, поэтому AB является хордой этой окружности, а точка T лежит на продолжении хорды AB, то есть вне окружности. Получаем противоречие, и этот случай невозможен.
Ответ: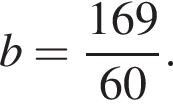
*Заметим, что для отрезков AB и OC, пересекающихся в точке T, условие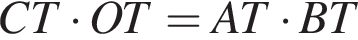 
является необходимым и достаточным условием того, что четыре точки A, B, C, O лежат на одной окружности.
Составлено уравнение хотя бы одного серединного перпендикулярна — 1 балл.
За нахождение координат точек пересечения прямой и параболы — баллы не добавляются.