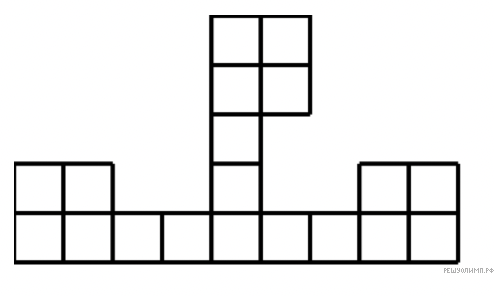
 Сколькими способами фигуру, изображенную на рисунке, можно раскрасить по клеткам в синий, белый и красный цвета так, чтобы соседние (то есть имеющие общие стороны) клетки были раскрашены в разные цвета?
Сколькими способами фигуру, изображенную на рисунке, можно раскрасить по клеткам в синий, белый и красный цвета так, чтобы соседние (то есть имеющие общие стороны) клетки были раскрашены в разные цвета?
Решение. Центральную клетку можно раскрасить тремя способами. После этого нам осталось раскрасить четыре одинаковых фигурки из шести клеток с одним и тем же ограничением на цвет клетки, соседней с центральной (назовём её клеткой А).
Рассмотрим квадрат  В таком квадрате должны быть две клетки одного цвета и расположены они должны быть по диагонали. Двумя способами выбираем диагональ, тремя способами её цвет и ещё по два способа на выбор цвета для остальных клеток, итого 24 способа. Однако при этом квадраты, покрашенные в два цвета мы посчитали дважды, поэтому остаётся 18 способом.
В таком квадрате должны быть две клетки одного цвета и расположены они должны быть по диагонали. Двумя способами выбираем диагональ, тремя способами её цвет и ещё по два способа на выбор цвета для остальных клеток, итого 24 способа. Однако при этом квадраты, покрашенные в два цвета мы посчитали дважды, поэтому остаётся 18 способом.
При этом, очевидно, для каждого из трёх цветов есть по 6 способов таких, что клетка, соседняя не только с клетками квадрата, имеет именно этот цвет. Эту клетку назовём клеткой Б. 31 Клетка А может быть покрашена двумя способами. Для каждого из этих способов есть 6 способов раскраски квадрата таких, что клетка Б покрашена в тот же цвет. Тогда клетку между ними можно покрасить двумя способами, итого  варианта.
варианта.
Кроме того, для каждого из способов покрасить клетку А есть 12 способов раскраски квадрата таких, что клетка Б имеет другой цвет. В этом случае клетка между ними красится однозначно, поэтому опять получаем 24 способа. Итого 48 способов раскраски каждой такой фигуры. Следовательно, ответ в задаче 
Ответ: 
Ответ: 
Аналоги к заданию № 891: 899 Все