Основанием пирамиды TABCD служит прямоугольник со сторонами AB = 12 и AD = 4, а боковые ребра соответственно равны TA = 3, TD = 5, TC = 13. Какую наименьшую площадь может иметь сечение пирамиды плоскостью, проходящей через вершину T, центр симметрии основания и точку M, лежащую на ребре BC? На какие части делит точка M ребро BC в этом случае?
Решение. При построении чертежа следует учесть следующее:  отсюда
отсюда

также 
 отсюда
отсюда

а так как DC, AB, TAD — перпендикулярны между собой, то  Следовательно, боковое ребро TA перпендикулярно ABCD.
Следовательно, боковое ребро TA перпендикулярно ABCD.
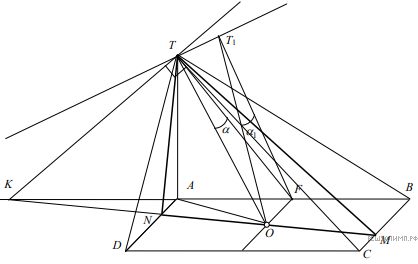
При любом положении точки M на стороне BC грань TAB является ортогональной проекцией сечения TMN. Площадь сечения будет наименьшей, если наименьшим будет угол между секущей плоскостью и гранью TAB. Так как секущая плоскость проходит через центр симметрии основания O и вершину пирамиды T, то отрезок OT является наклонной к плоскости грани TAB, и наименьшим возможным углом будет  где прямая OF перпендикулярна TAB,
где прямая OF перпендикулярна TAB,  Линия пересечения секущей плоскости и плоскости грани TAB: TK перпендикулярна TF и пересекает прямую AB в точке K. Если условие TK перпендикулярна TF не выполнено, то
Линия пересечения секущей плоскости и плоскости грани TAB: TK перпендикулярна TF и пересекает прямую AB в точке K. Если условие TK перпендикулярна TF не выполнено, то 

 и
и

Прямая, проведенная через точки K и O, пересекает ребро AD в точке N и ребро BC в точке M,  — искомое сечение.
— искомое сечение.
Если обозначить 

 то
то




В 
 и
и  тогда
тогда

Точка M делит отрезок BC в отношении

| AB | BC | TA | TF | TO |  | SNTM |  | BM | MC |
| 12 | 4 | 3 |  | 7 |  |  | 9 : 1 |  |  |
Ответ: наименьшая площадь сечения равна  точка M делит ребро BC на части —
точка M делит ребро BC на части — 
Ответ: наименьшая площадь сечения равна

точка
M делит ребро
BC на части —




