сайты - меню - вход - но­во­сти
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об олим­пи­а­дах
Ка­та­лог за­да­ний
Уче­ни­ку
Учи­те­лю
Школа
Ска­зать спа­си­бо
Во­прос — ответ


Задания
Версия для печати и копирования в MS Word

На сто­ро­нах AB, BC и CA тре­уголь­ни­ка ABC от­ме­че­ны точки C1, A1 и B1 со­от­вет­ствен­но. От­рез­ки AA1, BB1 и CC1 пе­ре­се­ка­ют­ся в точке P. Най­ди­те от­но­ше­ние A P: P A_1, если A B: A C_1= альфа боль­ше 1 и A C: A B_1= бета боль­ше 1.

Спрятать решение

Ре­ше­ние.

Так как A B: A C_1= альфа и A C: A B_1= бета , то

дробь: чис­ли­тель: A C_1, зна­ме­на­тель: C_1 B конец дроби = дробь: чис­ли­тель: 1, зна­ме­на­тель: альфа минус 1 конец дроби

и
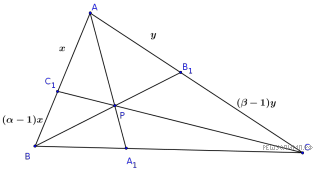
дробь: чис­ли­тель: A B_1, зна­ме­на­тель: B_1 C конец дроби = дробь: чис­ли­тель: 1, зна­ме­на­тель: бета минус 1 конец дроби .

За­пи­шем тео­ре­му Чевы для тре­уголь­ни­ка ABC и че­ви­ан AA1, BB1 и CC1:

дробь: чис­ли­тель: A C_1, зна­ме­на­тель: C_1 B конец дроби умно­жить на дробь: чис­ли­тель: B A_1, зна­ме­на­тель: A_1 C конец дроби умно­жить на дробь: чис­ли­тель: C B_1, зна­ме­на­тель: B_1 A конец дроби =1.

Сле­до­ва­тель­но,

дробь: чис­ли­тель: B A_1, зна­ме­на­тель: A_1 C конец дроби = дробь: чис­ли­тель: A B_1, зна­ме­на­тель: B_1 C конец дроби умно­жить на дробь: чис­ли­тель: B C_1, зна­ме­на­тель: C_1 A конец дроби = дробь: чис­ли­тель: альфа минус 1, зна­ме­на­тель: бета минус 1 конец дроби .

Оста­лось вос­поль­зо­вать­ся тео­ре­мой Ме­не­лая для AA1C и пря мой BB1:

дробь: чис­ли­тель: B A_1, зна­ме­на­тель: B C конец дроби умно­жить на дробь: чис­ли­тель: C B_1, зна­ме­на­тель: B_1 A конец дроби умно­жить на дробь: чис­ли­тель: A P, зна­ме­на­тель: P A_1 конец дроби =1

или

дробь: чис­ли­тель: A P, зна­ме­на­тель: P A_1 конец дроби = дробь: чис­ли­тель: B C, зна­ме­на­тель: B A_1 конец дроби умно­жить на дробь: чис­ли­тель: A B_1, зна­ме­на­тель: B_1 C конец дроби = левая круг­лая скоб­ка 1 плюс дробь: чис­ли­тель: бета минус 1, зна­ме­на­тель: альфа минус 1 конец дроби пра­вая круг­лая скоб­ка умно­жить на дробь: чис­ли­тель: 1, зна­ме­на­тель: бета минус 1 конец дроби = дробь: чис­ли­тель: 1, зна­ме­на­тель: альфа минус 1 конец дроби плюс дробь: чис­ли­тель: 1, зна­ме­на­тель: бета минус 1 конец дроби .

При­ве­дем дру­гое ре­ше­ние. При­ме­ним тео­ре­му Ван-Обеля:

дробь: чис­ли­тель: A P, зна­ме­на­тель: P A_1 конец дроби = дробь: чис­ли­тель: A C_1, зна­ме­на­тель: C_1 B конец дроби плюс дробь: чис­ли­тель: A B_1, зна­ме­на­тель: B_1 C конец дроби = дробь: чис­ли­тель: 1, зна­ме­на­тель: альфа минус 1 конец дроби плюс дробь: чис­ли­тель: 1, зна­ме­на­тель: бета минус 1 конец дроби .

Ответ: дробь: чис­ли­тель: 1, зна­ме­на­тель: альфа минус 1 конец дроби плюс дробь: чис­ли­тель: 1, зна­ме­на­тель: бета минус 1 конец дроби .

Спрятать решение · Помощь


О про­ек­те · Ре­дак­ция · Пра­во­вая ин­фор­ма­ция · О ре­кла­ме
© Гущин Д. Д., 2011—2024