Задания
Версия для печати и копирования в MS WordИзвестно, что углы A, B, C треугольника ABC удовлетворяют соотношению
Приведите хотя бы один пример такого треугольника, длины сторон которого: а) рациональны; б) действительны.
Решение. 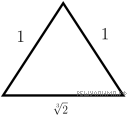
Заметим, что
и
Будем теперь преобразовывать левую часть данного в условии задачи равенства:
Итак, углы треугольника АВС связаны зависимостью
Преобразуем это равенство следующим образом:
Далее:
и
Это даёт нам:
Так как
то искомое соотношение между сторонами треугольника имеет вид:
при следовательно,
и
Ответ: a) ∅; б) да.



