Точки A1, B1, C1 — точки пересечения продолжений высот остроугольного треугольника ABC с описанной вокруг ABC окружностью. Окружность, вписанная в треугольник A1B1C1, касается одной из сторон ABC, а один из углов треугольника ABC равен 50°. Найдите два других угла треугольника ABC.
Решение. 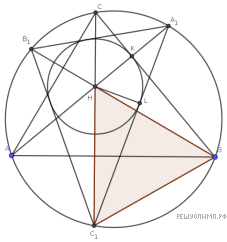 Не умаляя общности, пусть окружность ω, вписанная в A1B1C1, касается стороны BC. Пусть H — точка пересечения высот треугольника ABC, K — точка касания ω и BC, L — точка касания ω и A1C1. Мы собираем доказать, что треугольник HBC1 равносторонний. Тогда
Не умаляя общности, пусть окружность ω, вписанная в A1B1C1, касается стороны BC. Пусть H — точка пересечения высот треугольника ABC, K — точка касания ω и BC, L — точка касания ω и A1C1. Мы собираем доказать, что треугольник HBC1 равносторонний. Тогда

откуда с учётом условия и будет следовать ответ.
Для начата заметим, что H есть точка пересечения биссектрис треугольника A1B1C1. Действительно, например,

то есть C1H — биссектриса угла A1C1B1; аналогично проверяются и то, что A1H и B1H также являются биссектрисами соответствующих углов. Следовательно, H — центр вписанной окружности треугольника A1B1C1 и  Кроме того, выше доказано, что
Кроме того, выше доказано, что  то есть прямоугольные треугольники HC1L и HBK равны по катету и острому углу. Поэтому
то есть прямоугольные треугольники HC1L и HBK равны по катету и острому углу. Поэтому 
Осталось заметить, что  Этот факт хорошо известен и может быть доказан различными способами. Приведём здесь лишь один из них. Заметим, что треугольники
Этот факт хорошо известен и может быть доказан различными способами. Приведём здесь лишь один из них. Заметим, что треугольники  и
и  равны по стороне (общая сторон а AB) и двум углам
равны по стороне (общая сторон а AB) и двум углам

аналогично доказываем, что 
Ответ: 60° и 70°.
Критерии проверки:| Критерии оценивания | Балл |
|---|
| Верное решение без существенных недочетов | + |
| В целом задача решена, хотя и с недочетами | + − |
| Задача не решена, но есть заметное продвижение | − + |
| Задача не решена, заметных продвижений нет | − |
| Задача не решалась | 0 |
Ответ: 60° и 70°.



