В угол BCA вписана окружность радиуса 1 с центром в точке ܱO1. Синус угла O1CA равен  Вторая окружность касается первой окружности и сторон угла. Найдите радиус третьей окружности, которая касается двух данных окружностей и одной из сторон угла.
Вторая окружность касается первой окружности и сторон угла. Найдите радиус третьей окружности, которая касается двух данных окружностей и одной из сторон угла.
Решение. 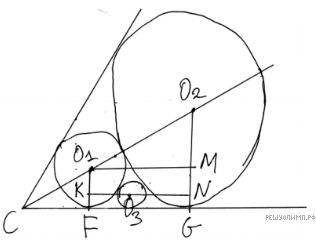
Как известно, центр окружности, вписанной в угол, лежит на биссектрисе угла. Пусть C — вершина угла, O1 — центр первой окружности.
Ситуация один: центр второй окружности O2 лежит за пределами отрезка CO1 (см. рис. верхний). Пусть F — точка касания первой окружности (с центром O1) с одной из сторон угла, a G — точка касания второй окружности (с центром O2) с той же стороной угла, P — точка касания этих окружностей. По условию:

Тогда из прямоугольного треугольника O1CF:  а CP = 4.
а CP = 4.
Пусть радиус окружности с центром O2 равен R. Тогда  и
и  Из прямоугольного треугольника O2CG получаем:
Из прямоугольного треугольника O2CG получаем:  т. е.
т. е.  откуда R = 2. Найдём отрезок FG. Для этого проведём через центр первой окружности O1 перпендикуляр O1M на радиус O2G. Тогда в прямоугольном треугольнике O1MO2:
откуда R = 2. Найдём отрезок FG. Для этого проведём через центр первой окружности O1 перпендикуляр O1M на радиус O2G. Тогда в прямоугольном треугольнике O1MO2:

и

Тогда по теореме Пифагора:

Теперь через центр искомой третьей окружности O3 проведём прямую, параллельную прямой FG. Пусть эта прямая пересекает радиус O1F в точке K, а радиус O2G в точке N. Рассмотрим прямоугольный треугольник O1KO3. Обозначим радиус искомой окружности r. Тогда  и
и  По теореме Пифагора:
По теореме Пифагора:

А теперь из прямоугольного треугольника O3NO2 имеем:

и

По теореме Пифагора:

Так как:  то
то  откуда:
откуда:

и

Другой вариант записи ответа:


Ситуация два: центр второй окружности O2 лежит на отрезке CO1 (см. рис. нижний). В этом случае получится картинка, подобная той, что была в ситуации один (см. рис. верхний), но теперь большей будет первая окружность (с центром O1). Коэффициент подобия картинок равен  поэтому легко рассчитать все элементы чертежа, включая ответ. Так,
поэтому легко рассчитать все элементы чертежа, включая ответ. Так, 
 и
и 
Другой вариант записи ответа:

Ответ:  или
или 
Критерии проверки:| Критерии | Баллы |
|---|
| Обоснованно получены верные ответы в обеих ситуациях | 15 |
| Обоснованно получен верный ответ только в одной из ситуаций | 10 |
| Сделаны существенные продвижения в решении задачи, например, хотя бы в одной из ситуаций верно найден радиус второй окружности и отрезок FG (или равный ему отрезок), но не найден ни один верный ответ ни в одной из ситуаций | 5 |
| Все остальные случаи | 0 |
Ответ: 
или

Вторая окружность касается первой окружности и сторон угла. Найдите радиус третьей окружности, которая касается двух данных окружностей и одной из сторон угла.



