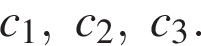В условии этой задачи все числа — комплексные.
а) Нарисуйте образ полуплоскости 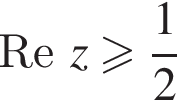 при отображении, сопоставляющем числу z число
при отображении, сопоставляющем числу z число ![]()
б) Докажите, что если 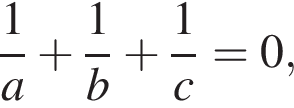 то треугольник с вершинами в точках a, b, c содержит начало координат.
то треугольник с вершинами в точках a, b, c содержит начало координат.
в) Докажите, что всякий корень уравнения
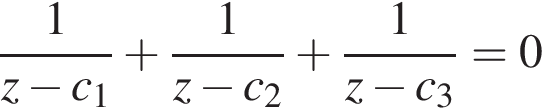
лежит в треугольнике с вершинами в точках 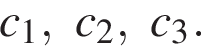
Решение. а) Ответ: — на рисунке. Пусть
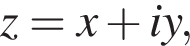
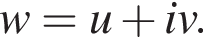 Поскольку
Поскольку 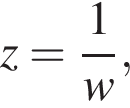 то
то 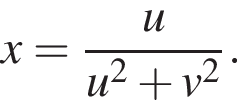 Точка w принадлежит образу полуплоскости
Точка w принадлежит образу полуплоскости ![]() тогда и только тогда, когда
тогда и только тогда, когда
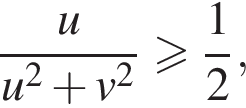


б) Одно из возможных решений: если 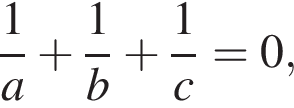 то
то 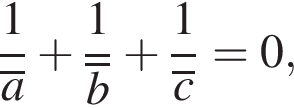
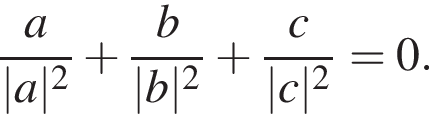
Последнее равенство имеет вид  где
где 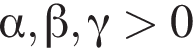 и
и  таким образом, начало координат лежит внутри выпуклой оболочки точек a, b, c,
таким образом, начало координат лежит внутри выпуклой оболочки точек a, b, c,
в) Если ![]() — корень уравнения,
— корень уравнения, 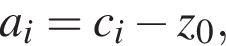 то
то
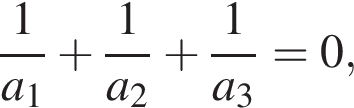
в силу утверждения предыдущего пункта точка ноль лежит внутри треугольника с вершинами 
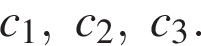
| За каждый из четырех пунктов сюжета выставляется одна из следующих оценок: + (3 балла), ± (2 балла), ∓ (1 балл), − (0 баллов) Максимум за сюжет 12 баллов. При этом необходимо руководствоваться следующим. | |
| Критерии оценивания выполнения заданий | Баллы |
|---|---|
| Верное и полное выполнение задания | 3 |
| Ход решения верный, решение доведено до ответа, но допущен один недочет | 2 |
| Ход решения верный, решение доведено до ответа, но допущено два недочета или одна грубая ошибка | 1 |
| Остальные случаи | 0 |
| К недочетам относятся, например: описки, неточности в использовании математической символики; погрешности на рисунках, недостаточно полные обоснования; неточности в логике рассуждений при сравнении чисел, доказательстве тождеств или неравенств; вычислительные ошибки, не повлиявшие принципиально на ход решения и не упростившие задачу, если задача не являлась вычислительной; замена строго знака неравенства нестрогим или наоборот; неверное присоединение либо исключение граничной точки из промежутка монотонности и аналогичные. Грубыми ошибками являются, например: потеря или приобретение постороннего корня; неверный отбор решения на промежутке при правильном решении в общем виде; вычислительная ошибка в задаче на вычисление; неверное изменение знака неравенства при умножении на отрицательное число, логарифмировании или потенцировании и т. п. | |
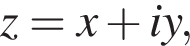
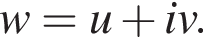 Поскольку
Поскольку 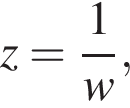 то
то 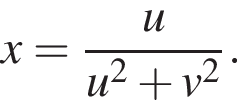 Точка w принадлежит образу полуплоскости
Точка w принадлежит образу полуплоскости 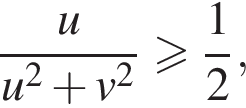


б) Одно из возможных решений: если 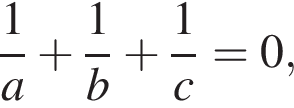 то
то 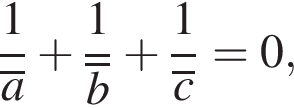
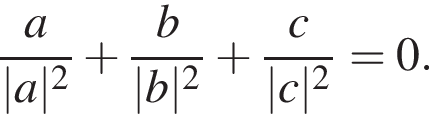
Последнее равенство имеет вид  где
где 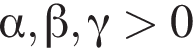 и
и  таким образом, начало координат лежит внутри выпуклой оболочки точек a, b, c,
таким образом, начало координат лежит внутри выпуклой оболочки точек a, b, c,
в) Если ![]() — корень уравнения,
— корень уравнения, 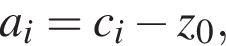 то
то
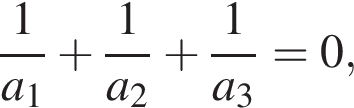
в силу утверждения предыдущего пункта точка ноль лежит внутри треугольника с вершинами 
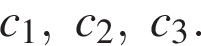
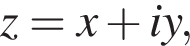
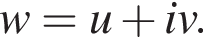 Поскольку
Поскольку 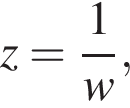 то
то 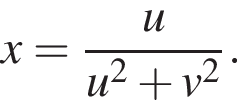 Точка w принадлежит образу полуплоскости
Точка w принадлежит образу полуплоскости 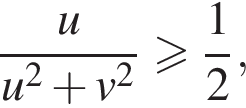


б) Одно из возможных решений: если 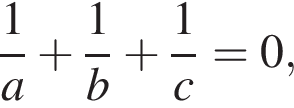 то
то 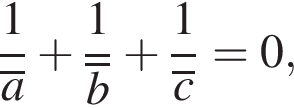
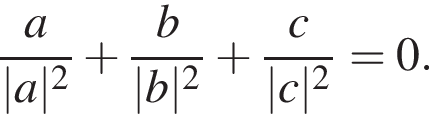
Последнее равенство имеет вид  где
где 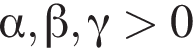 и
и  таким образом, начало координат лежит внутри выпуклой оболочки точек a, b, c,
таким образом, начало координат лежит внутри выпуклой оболочки точек a, b, c,
в) Если ![]() — корень уравнения,
— корень уравнения, 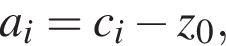 то
то
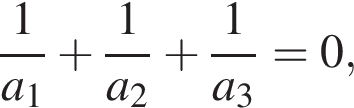
в силу утверждения предыдущего пункта точка ноль лежит внутри треугольника с вершинами